√画像をダウンロード (a-b)^3+(b-c)^3+(c-a)^3 125303-(a+b-2c)^3+(b+c-2a)^3+(c+a-2b)^3
Cho a,b,c là ba cạnh của tam giácC/m$(abc)(bca)(cab)\leq abc$ posted in Bất đẳng thức và cực trị Cho a, b, c là độ dài ba cạnh của tam giác Chứng minh a) $(abc)(bca)(cab)\leq abc$ b) $\frac{a}{bca}\frac{b}{acb}\frac{c}{abc}\geq 3$Nếu bạn hỏi, bạn chỉ thu về một câu trả lời Nhưng khi bạn suy nghĩ trả lời, bạn sẽ thu về gấp bội!Example Solve 8a 3 27b 3 125c 3 30abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 30abc) can be written as (2a) 3 (3b) 3 (5c) 3 (2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc

Ex 9 1 3 I Add Ab Ca Ca Ab Chapter 9 Class 8
(a+b-2c)^3+(b+c-2a)^3+(c+a-2b)^3
(a+b-2c)^3+(b+c-2a)^3+(c+a-2b)^3-Learn with Tiger how to do (a/b)^3(b/c)^3(c/a)^33 fractions in a clear and easy way Equivalent Fractions,Least Common Denominator, Reducing (Simplifying) Fractions Tiger Algebra Solver3(bc)(ca)(ab) If we use the following Result, we can immediately factorise the given Exp=3(bc)(ca)(ab) Result xyz=0 rArr x^3y^3z^3=3xyz Otherwise, consider the following Let, u=bc, v=ca rArr uv=ba=(ab) Now, The Exp=u^3v^3{(uv)}^3, =u^3v^3(uv)^3, =u^3v^3{u^3v^33uv(uv)}, =3uv(uv)=3uv{(uv)}, "
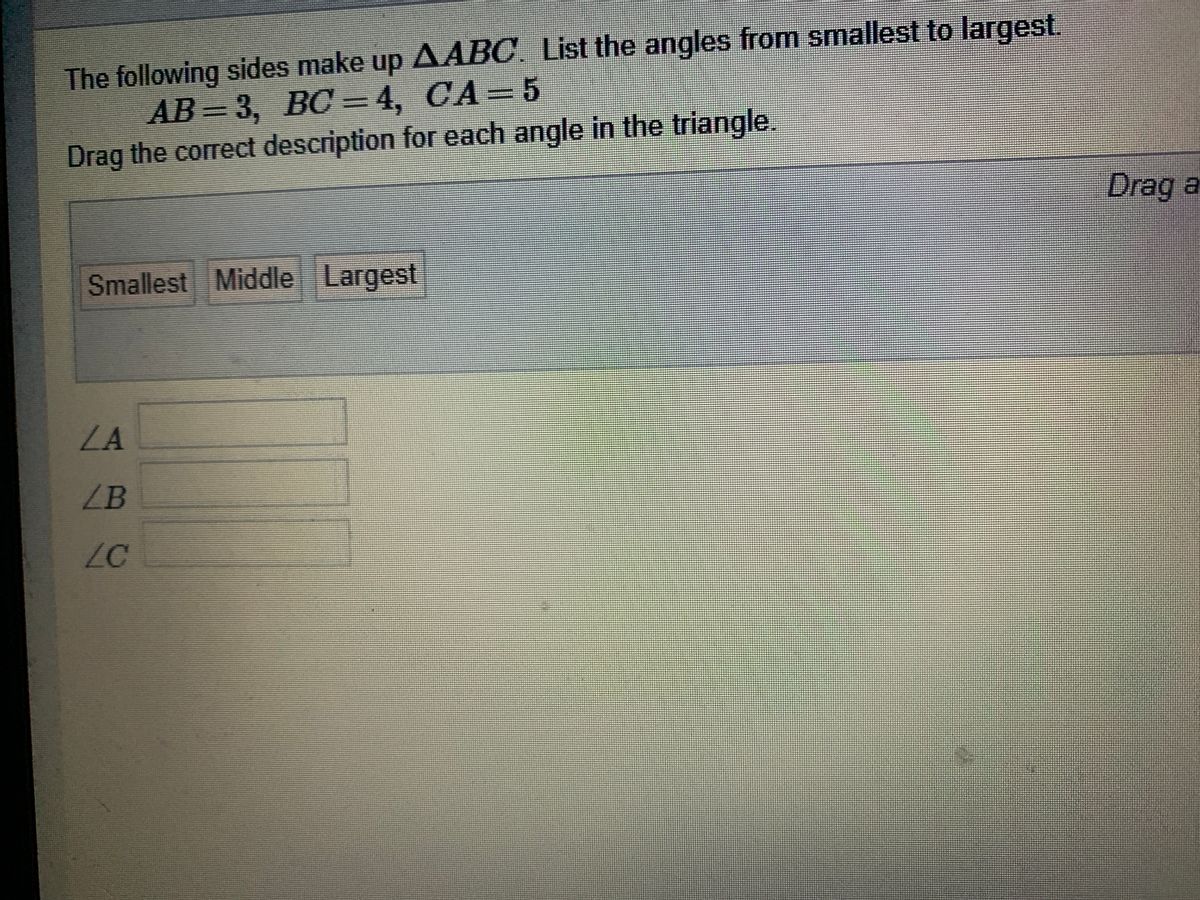


Answered The Following Sides Make Up bc List Bartleby
X^3y^3z^3 = (xyz)(x^2y^2z^2xy xz yz) 3xyz is a identity/ You may prove by simple foiling for x = a^(1/3) and y = b^(1/3) and z = c^(1/3) you getA3 b3 c3 = (a b c) (a2 b2 c2 – ab – bc – ca) 3abcIf (ab)(bc)(ca)= 233 and (abc)= 16, then the value of c is CORRECT ANSWER 8 Enter the code shown above (Note If you cannot read the numbers in the above image, reload the page to generate a new one)
Question to simplify(a 2b 2) 3 (b 2c 2) 3 (c 2a 2) 3 / (ab) 3 (bc) 3 (ca) 3 Answer Let's solve the numerator first if abc = 0 Then a 3 b 3 c 3 = 3abc Now,(a 2b 2) 3 (b 2c 2) 3 (c 2a 2) 3 = a 2b 2 b 2c 2 c 2a 2 = 0 That means we can use this formula here because abc is coming out to be zeroHowever, there is a problem when trying to prove (abc)^2 ≤ 3(abbcca), because, in fact, the opposite is true (abc)^2 ≥ 3(abbcca) You can see that if you expand (abc)^2, simplify, multiply by 2, and use the trivial inequalityX^3y^3z^3 = (xyz)(x^2y^2z^2xy xz yz) 3xyz is a identity/ You may prove by simple foiling for x = a^(1/3) and y = b^(1/3) and z = c^(1/3) you get
3a^3 = 3a^3, a true equation Thus, a = b = c is always a solution, and abc = 3a = 3b = 3c Also, c = a b is a solution a^3 b^3 (a b)^3 = a^3 b^3 a^3 3a^2*b 3a*b^2 b^3 =3a^2*b 3a*b^2 =a*(3ab) b*(3ab) = 3ab * (a b) = 3abc Then abc = ab(ab) = 0Then take c=a and also sheres on ca(abc)^3a^3b^3c^3 =k(ab)(bc)(ca) K is unknown, so find her If a=1,b=1,c=0》(110)^31^31^30=k (11)(10)(01) =k*2 K=3 (abc)^3a^3b^3c^3 =3 (ab)(bc)(ca) October 29, 15 at 841 PM Unknown said See this one((ab)c)^3a^3b^3c^3The formula is (xy)^3 = x^3 3x^2y 3xy^2 y^3 Expand (ab)^3 = a^3 3a^2b 3ab^2 b^3 Expand (bc)^3 = b^3 3b^2c 3bc^2 c^3 Expand (ca)^3 = c^3 3c^2a 3ca^2 a^3 = c^3



Add The Following 4ab 5bc 7ca 3ab 2bc 3ca 5ab 3bc 4ca


Www Selfstudys Com Uploads Pdf Qylgkjm8rri5luafbgjk Pdf
This fulllength music video of ABCmouse's cover version of "ABC" by The Jackson 5 features moreA^3(bc)b^3(ca)c^3(ab) This deals with simplification or other simple resultsAll equal mod 3, in which case the second factor is clearly divisible by 3, or A;B;C are all di erent mod 3, in which case (A 2B) (B C) 2 (C A) is equal to 1 1 1 modulo 3 and the second factor is again divisible by 3



Factorise A3 B C 3 C A 3 C3 A B 3 Math Polynomials Meritnation Com



If If A B C Are All Non Zero And A B C 0 Prove That B2 Ca C2 Ab 3 Mathematics Topperlearning Com 2jnu5w66
Click here👆to get an answer to your question ️ Prove that (a b c)^3 a^3 b^3 c^3 = 3(a b ) (b c) (c a)A/3 = 3 (B C)/3 = (BC) = BC Now, from here it's pretty easy You want to get B by itself so you want to get C on the other side of the equation Remember whatever you do on one side, you must do on the other side So, subtract C from both sides (A/3) C = B C C = B There is your answer B = (A/3) CThis fulllength music video of ABCmouse's cover version of "ABC" by The Jackson 5 features more



If The Vertices A B C Of A Triangle Abc Are 1 2 3 1 0 0 0 1 2 Respectively Then Find Abc Abc Is The Angle Between The Vectors Bar Ba And Bar Mathematics Shaalaa Com


Math Education Geometry Problem 809 Trisecting A Line Segment Ab 3 Circles Radius Center Level High School Honors Geometry College Mathematics Education Distance Learning
For example, we can write $(ABC)' \equiv \big(A (BC)\big)' \equiv \big(A' \cdot (BC)'\big) \equiv A'\cdot (B'C') \equiv A'B'C'$ Indeed, provided we have a negated series of multiple variables all connected by the SAME connective (all and'ed or all or'ed), we can generalize DeMorgan's to even more than three variables, again, due to theChứng minh rằng (abc)^3 = a^3 b^3 c^3 3(a b)(b c)(c a) với mọi a, b, c bằng 3 cách Cách số 1 Khai triển vế trái thành vế phảiExample 1 Solve (4p 5q 3r) 2 Solution This proceeds as Given polynomial (4p 5q 3r) 2 represents identity first ie (a b c) 2 Where a = 4p, b = 5q and c = 3r Now apply values of a, b and c on the identity ie (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca and we get (4p 5q 3r) 2 = (4p) 2 (5q) 2 (3r) 2 2(4p)(5q) 2(5q)(3r) 2(3r)(4p) Expand the exponential forms



If A 2 B 2 C 2 250 And Ab Ca 3 Then Find A B C


2
Learning can truly be as easy as ABC, 123, and DoReMi!Bài 3 Ta có \(a^2b^2c^2=3\ge abbcca\) ( tự cm bđt nha ) Áp dụng bất đẳng thức Schwarz ta có \(\dfrac{a^3}{bc}\dfrac{b^3}{ca}\dfrac{c^3}{abThe Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Explanation Let us just start with (abc)² = a² b² c²2ab2bc2ca



Question Prove That A B C 3 A3 C3 3 A B B C C A Mathematics Topperlearning Com We5wwhmm


2
Prove (a b)^3 (b c)^3 (c a)^3 = 3(ab)(bc)(ca) without expanding using the Multivariable Factor Theorem Guest Aug 21, 18 0 users composing answers(ab) 3 (bc) 3 (ca) 3 Let, a = ab b = bc c = ca then, abc = abbcca = 0 therefore, a 3 b 3 c 3 =3abc =3(ab)(bc)(ca)If a = b = c, then we get a^3 a^3 a^3 = 3*a*a*a;



A Few Variants Of A Popular Inequality And A Generalization



D O Mv 18 There Is A Flat Uniform Triangular Plate Abc Physics
By using above equation let us consider a = a, b= b and c = c Then the equation (10 BECOMES a 3 (b 3) (c 3) − 3a (b) (c) = (a b c) (a 2 (b 2) (c 2) − a (b) − (b) (c) − (c)a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 ab – bc ca)Prove (a b)^3 (b c)^3 (c a)^3 = 3(ab)(bc)(ca) without expanding using the Multivariable Factor Theorem Guest Aug 21, 18 0 users composing answersSolve for c A=(abc)/3 Rewrite the equation as Multiply both sides of the equation by Cancel the common factor of Tap for more steps Cancel the common factor Rewrite the expression Move all terms not containing to the right side of the equation Tap for more steps



Ab 4 3 Ca 2 の Abcがあり Bacの二等分線と辺bcの交点をd Abcの 高校 教えて Goo



Factorise A B 3 B C 3 C A 3 Thanks Math Polynomials Meritnation Com
Learning can truly be as easy as ABC, 123, and DoReMi!By using above equation let us consider a = a, b= b and c = c Then the equation (10 BECOMES a 3 (b 3) (c 3) − 3a (b) (c) = (a b c) (a 2 (b 2) (c 2) − a (b) − (b) (c) − (c)a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 ab – bc ca)Your approach is intuitive and that was also the first thing I thought;



If A B C 250 And Ab Ca 3 Then What Will Be The Value Of A B C Quora



Find The Area Of A Quadrilateral Abcd In Which Ab 3 Cm 4 Cm Cd 4 Cm Cbse Class 9 Maths Learn Cbse Forum
Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (ab)^3(bc)^3(ca)^3(ab)(bc)(ca) so that you understand betterChapter 3 CAB ECC and AHA 10 updates changed the CPR sequence from ABC to CAB Often in the ABC method chest compressions were delayed With the new Compressions – Airway – Breathing method a victim receives compressions faster, providing quicker critical blood flow to the vital organsAs stated in the title, I'm supposed to show that $(abc)^3 = a^3 b^3 c^3 (abc)(abacbc)$ My reasoning $$(a b c)^3 = (a b) c^3 = (a b)^3 3(a b)^2c 3(a b)c^2 c^3 Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers



Solved Etisalat 2 16 Pm Dld Questions Pdf 325 Kb Close I Chegg Com


Q Tbn And9gcstdrjoblzm8 K6zg8rxa0tub Ect0kmewckvckrn6ybypcdio0 Usqp Cau
We can write \((abc)^3 = (abc)(abc)(abc) \) \(=>(abc)^3 = (abc)^2 (abc) \) we know that what is the formula of \( (abc)^2 \) \(=>(abc)^3 = (a^2b^2c^2 2ab 2bc 2ca) (abc) \)2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32Tiger was unable to solve based on your input (ab)3 (bc)3 (ca)3 Step by step solution Step 1 11 Evaluate (ca)3 = c33ac23a2ca3 Step 2 Pulling out like terms 21 (ab)^3 (ab)^32b^3 (ab)3 −(a −b)3 −2b3 https//wwwtigeralgebracom/drill/ (a_b)~3 (ab)~32b~3/



Prove That The Above Determinant Ab Ca 3 Math Meritnation Com



Cho Cac Số Nguyen A B C Thỏa Man A B C A B B C C A Chứng Minh Rằng A B 3 B C 3 C A 3 Chia Hết Cho 81
Cách 1 Bạn nhóm $(ab)c^3$ lại rồi dùng hẳng đẳng thức phân tích như bình thường thôi P/s lát nữa mình edit bài viết ghi chi tiết sauThere are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –A^3(bc)b^3(ca)c^3(ab) This deals with simplification or other simple results



567 t Hay Va Kho


Q Tbn And9gcsn3hmt8qz Utmzoqeyjo2k4rnk95kuib8fxbhmd Uvs2llqap Usqp Cau
Please refer to the Explanation It is known that, (ab)^3=a^3b^33ab(ab) a^3b^3=(ab)^33ab(ab)(star) Setting, (ab)=d," we have, "a^3b^3=d^33abdI can do this better)if you take a=b,and you will see (bbc)^3(b)^3b^3c^3=c^3c^3=0,so (abc)^3a^3b^3c^3 shares on (ab) Bezout 's theoremthen take b=c and also sheres on bc Then take c=a and also sheres on ca(abc)^3a^3b^3c^3 =k(ab)(bc)(ca)Nếu bạn hỏi, bạn chỉ thu về một câu trả lời Nhưng khi bạn suy nghĩ trả lời, bạn sẽ thu về gấp bội!


Cbse 10 Math Cbse Coordinate Geometry Ncert Solutions


B B C Ca In Gp Prove See How To Solve It At Qanda
A 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc Some not so Common FormulasThere are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –Example Solve 8a 3 27b 3 125c 3 30abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 30abc) can be written as (2a) 3 (3b) 3 (5c) 3 (2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc


Nph Onlinelibrary Wiley Com Doi Pdf 10 1111 J 1469 8137 1992 Tb X
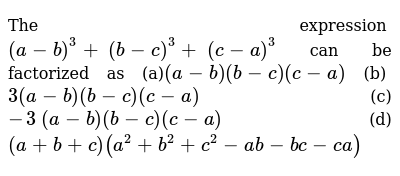


The Expression A B 3 B C 3 C A 3 Can Be Factorized A
If a b c = 0, the prove that a × b = b × c = c × a where a, b, c are nonzero vectors View solution If a and b are vectors such that ∣ a b ∣ = 2 9 and a × ( 2 i ^ 3 j ^ 4 k ^ ) = ( 2 i ^ 3 j ^ 4 k ^ ) × b , then a possible value of ( a b ) ⋅ ( − 7 i ^ 2 j ^ 3 k ^ ) isClick here👆to get an answer to your question ️ In a Δ ABC , prove that sin^3 A cos(B C) sin^3 B cos(C A) sin^3 C cos(A B) = 3sin Asin Bsin CSolution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3 (2a) (3b) (5c) And this represents identity a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c
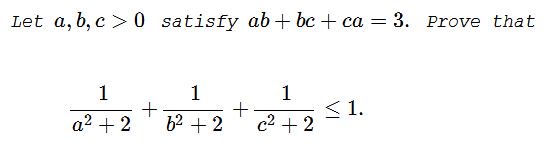


Alexander Bogomolny I Am Sorry What Does This Show That The Two Regions 3 And G 1 Coincide



A B 3 B C 3 C A 3 Is Equal To
Views around the world You can reuse this answer Creative Commons License
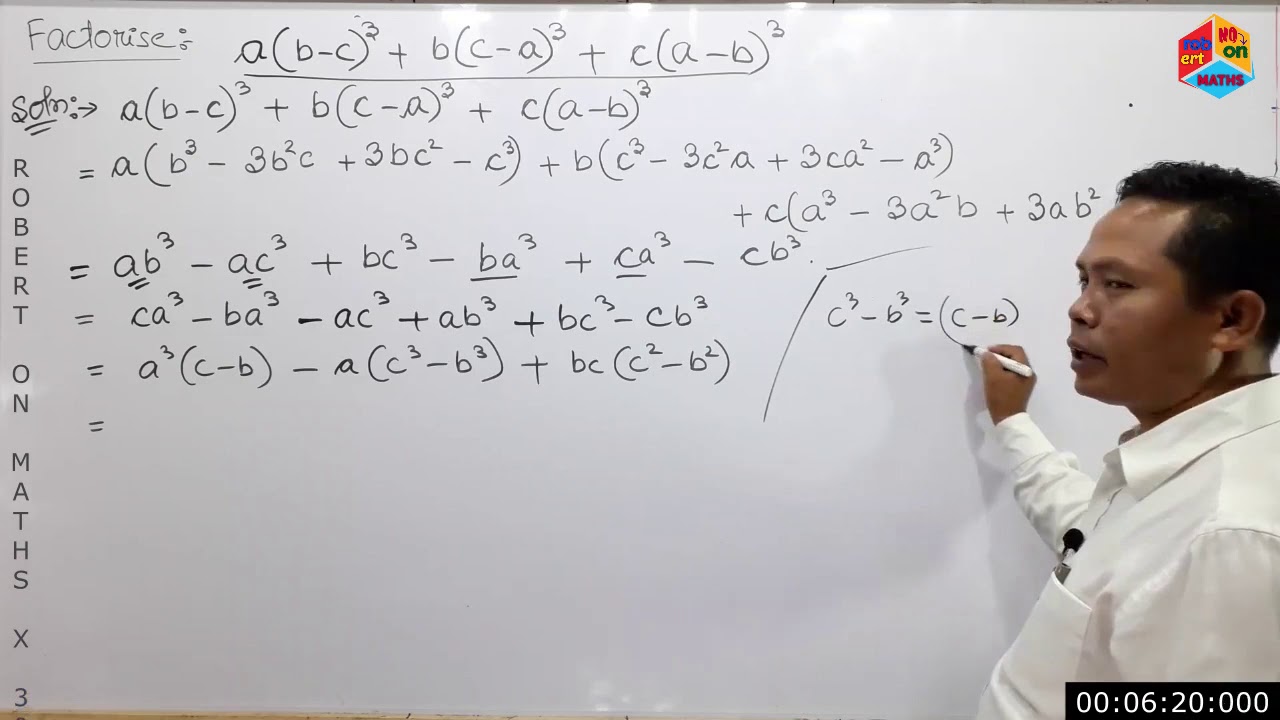


Maths X 3006b Factorisation Factorise A B C 3 B C A 3 C A B 3 Youtube



Ex 9 4 3 Viii Simplify A B C A B C Chapter 9 Class 8


Search Q A 5e3 2bb 5e3 2bc 5e3 3abc Formula Tbm Isch



How Prove Frac A 2 A 2b 2 Frac B 2 B 2c 2 Frac C 2 C 2a 2 Ge 1 Mathematics Stack Exchange



A B 3 B C 3 C A 3 A B B C C A A B B C C A



Razlozhit Na Mnozhiteli A B 3 B C 3 C A 3 Shkolnye Znaniya Com


Class 9 A 3 B 3 C 3



Answered The Following Sides Make Up bc List Bartleby



Show That A B 3 B C 3 C A 3 3 A B B C C A Brainly In



16 If A B 3 And B C 5 Then The Value Of B2 C2 Ab B Scholr



最新ab Ca ただぬりえ



A B 3 B C 3 C A 3 Is Equal To



Michael Rozenberg S Inequality In Three Variables With Constraints



Cos Cos Ca Cos Ab 3 2 Prove That Cosa Cosb Cosc 0



Factorise A B 3 B C 3 C A 3 Math Polynomials Meritnation Com


2
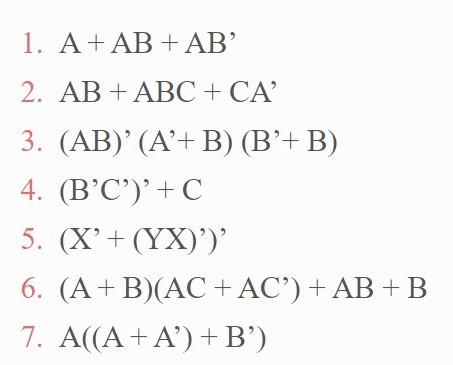


Solved 1 A Ab Ab 2 Ab Abc Ca 3 Ab A B Chegg Com
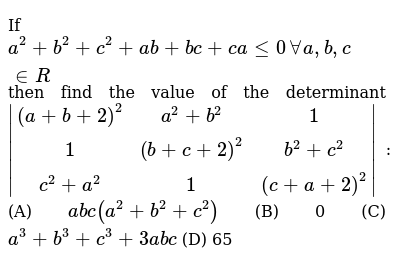


If A 2 B 2 C 2 Ab Ca 0 A B C In R Then Find The Value O


2



3 C B



Cau Hỏi Của Dương Thị Thu Ngọc Toan Lớp 8 Học Trực Tuyến
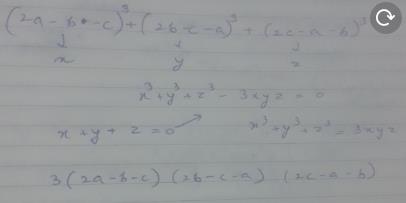


Factorize 2a B C 3 2b C A 3 2c A B 3 Answer This With Explanation Edurev Class 9 Question


2



A B 3 B C 3 C A 3


Simplify A 2 B 2 3 B 2 C 2 3 C 2 A 2 3 A B 3 B C 3 C A 3 Sarthaks Econnect Largest Online Education Community



The Shape Shifting Triangle Puzzle Mind Your Decisions



B2 3 B2 C2 3 C2 3 A B 3 B C 3 C A 3



567 t Hay Va Kho



Pdf 100 Inequalities Problems Amir Parvardi Academia Edu



The Expression A B 3 B C 3 C A 3 Can Be Factorized As A A B B C C A B 3 Youtube


Class Iv Mathematics Ppt Download



Be B C2 Be C Ac Ni Ac A A 6 Ab B2 Ab Ab 2 A Scholr



If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum



A B 3 B C 3 C A 3



Prove That A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2



Show That A B 3 B C 3 C A 3 3 A B B C C A Brainly In



Ex 9 1 3 I Add Ab Ca Ca Ab Chapter 9 Class 8



Factorise A 3 B C 3 B 3 C A 3 C 3 A B 3



Rut Gọn A A 3 B 3 C 3 3abc A B 3 B C 3 C A 3 Mai Trang



Solved This Is For Logic Class I Do Not Sure If Anyone C Chegg Com



Express A B 3 B C 3 C A 3 As A Product Of Its Factors Plszzzzzzzzzzzzzzzz Zzzzzzzzzzzzzzzzz Zzzzzzzzzzzzzzzzzz Answerz Zzzzzzzzz Plzzzz Zzzzzzz Tomorrow Math Meritnation Com



Using Properties Of Determinants Prove That 3a A B A C B A 3b B C C A C B 3c 3 A B C Ab Ca Mathematics Shaalaa Com



What Are Various Forms To Write A B C A Whole Cube Quora


Prove That A B C 3 A3 C3 3 A B B C C A Studyrankersonline



Factorise A B 3 B C 3 C A 3 Brainly In



Factorise 2a B C 3 2b C A 3 2c A B 3 Brainly In


Applying Am Gm In The Denominator After Flipping The Sign Chaitanya S Random Pages


View Question Prove A B 3 B C 3 C A 3 3 A B B C C A



Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A Youtube



3 C B



最新ab Ca ただぬりえ


If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline


Www Stmarysguwahati Org In Notes1 9 Ad Maths Pdf


因数分解でa B C 3 B C A 3 C A B 3 Yahoo 知恵袋


Http Services Aops Com Download Php Id Yxr0ywnobwvudhmvyi80lzg3mge4ywm2ntbkmtfjy2q4nmi4zwfinzu5mgvkmgm2nje2otjllnbkzg Rn Q2hhchrlciaynsbbts1htsbjbmvxdwfsaxrpzxmucgrm



Factorize I A B 3 B C 3 C A 3 Ii X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3 Youtube
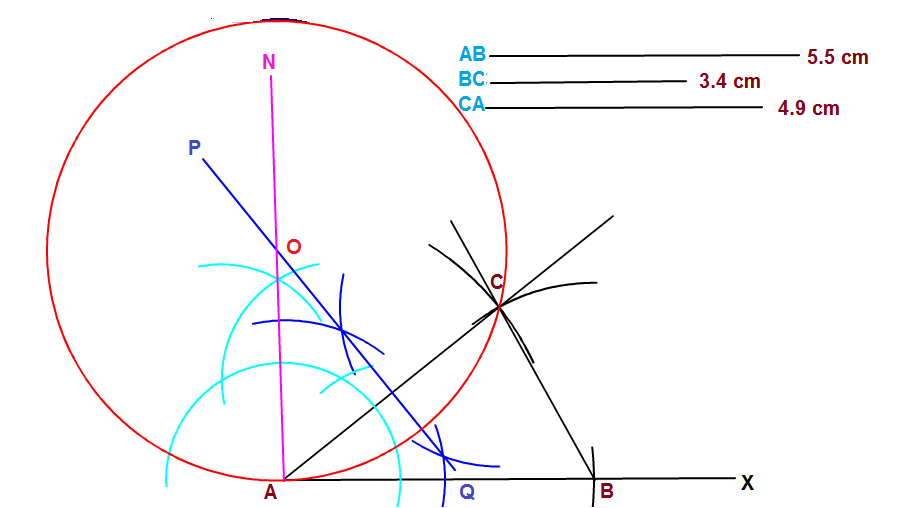


Using Ruler And Compass Construct 1 A Triangle Abc In Which Ab 5 5cm 3 4cm And Ca 4 9cm 2 Locus Of Points Equidistant From A And C 3 A Circle Touching Ab At A And Passing Through C



A B 3 B C 3 C A 3 Is Equal To


2



Simplify A 2 B 2 3 B 2 C 2 3 C 2 A 2 3 A B 3 B C 3 C A 3 Brainly In


2


Simplify A 2 B 2 3 B 2 C 2 3 C 2 A 2 3 A B 3 B C 3 C A 3 Sarthaks Econnect Largest Online Education Community


What Is The Expansion Of A B C 3 Quora



If Cos A B Cos B C Cos C A 3 2 Prove That Cosa Cosb Cosc Askiitians



Factorise A B 3 B C 3 C A 3 Brainly In
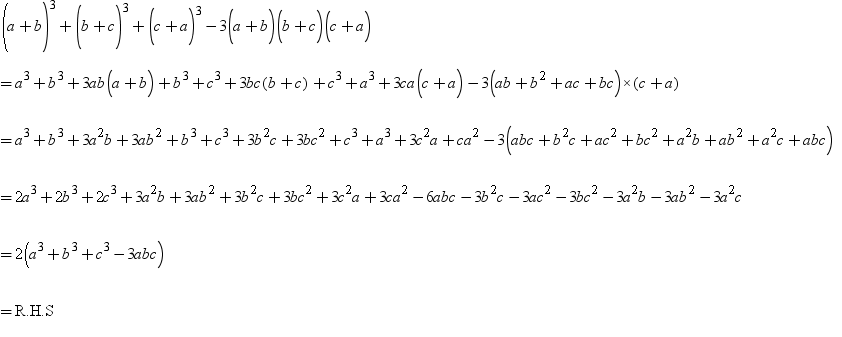


Q11 Prove That A B 3 B C 3 C A 3 3 Ab B C C A Scholr



What Will Be A B C If A B C 1 And Ab Ca 1 3 Quora


Ab Ac B2 See How To Solve It At Qanda



Rut Gọn A A 3 B 3 C 3 3abc A B 3 B C 3 C A 3 Mai Trang



A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Ac B 3 A B B C C A C Youtube



Student Community Question


Using Properties Of Determinants Prove That B 2 C 2 A 2 Ac Ac C 2 Ac A 2 Ab B 2 Ab Ab Ab Ac 3 Sarthaks Econnect Largest Online Education Community



2 Cho Cac Số Dương A B C Chứng Minh A 8 B 4 B 8 C 4 C 8 A 4 Lớn Hơn Bằng Ab 3 3 Ca 3 3 Cho Cac Số Dương A B C Chứng Minh A 4 B 2 C 2 B 4 C 2 A 2 C 4 A



最新ab Ca ただぬりえ



Prove That 1 1 1 A 2 B 2 C 2 A 3 B 3 C 3 A B B C C A Ab Ca



Inequalities From The Word 1995 05


コメント
コメントを投稿