コンプリート！ ガウス の 公式 958880

表32 ガウス・ルジャンドル積分公式 C Fortran90;※「ガウスの公式」について言及している用語解説の一部を掲載しています。 出典｜ 株式会社平凡社 世界大百科事典 第2版について 情報 関連語をあわせて調べるガウス記号の定義と3つの性質 レベル ★ 最難関大受験対策;

磁場公式b 磁場に関するガウスの法則 Lorett

ガウス の 公式

ガウス の 公式-この式で \(\alpha=a\,(\gt0),\ \beta=0\) と置くとガウス積分\eqref{gauss}になるから、\(I(\alpha,\beta)\) はガウス積分の一般化である。式\eqref{gauss}に \(a\gt0\) という条件が付いていることから予想されるように \(I(\alpha,\beta)\) は任意の複素数 \(\alpha,\beta\) について収束するわけではない。そこで、まずは積分ガウス積分の公式 2 したがって， I2 = e−ax2dx)2 e−ax2dx e−ay2dy dx ∫ ∞ −∞ dy e−a(x2y2) (3) と変形していくことができます． ここでx = rcosθ ，y = rsinθ と変数変換をします．また，無限遠で積分領域を矩形から円形 へと変形します．被積分関数が無限遠で速やかに0 に収束することから，この

ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門

B ガウスの公式の証明 25 C ルジャンドルの関係式の証明 29 0 はじめに 人類は何千年も前から円周率を求めようしてきた。円周の素朴な実測や，円の面 積を小さな正方形のマス目の数で求めることによっては，314まで求めることも困 難である．実際，円筒形のものに糸を巻き付けて，糸の長さと被積分関数f(x)は、解析的であることと周期関数でないことを前提としています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 ガウスルジャンドル数値積分 1ガウス求積（ガウスきゅうせき、英 Gaussian quadrature ）またはガウスの数値積分公式とは、カール・フリードリヒ・ガウスに因んで名づけられた数値解析における数値積分法の一種であり、実数のある閉区間(慣例的に −1, 1 に標準化される)で定義された実数値関数のその閉区間に渡る定積分値

ここまでできる科学技術計算 第2版 楽天： Excelで操る!ガウス関数（1） Gaussian のフーリエ変換は Gaussian 参考文献：篠崎、富山、若林「現代工学のための応用フーリエ解析」 p81、現代工学社 ( ) ( ) ( ) 2 exp2 4 f t vt F v v πω ω =−↔ = − 偶関数の場合：積分公式を利用 ( ) ( ) ( ) 22 ( ) 2 2 2,2 , exp cos exp 4 cos 2 exp 4 it ax∞ −∞ dxe−αx2 I2 = dxe−αx2 dye−αy2 = dx!

ガウス積分ガウス・ルジャンドルの公式 1 ガウス・ルジャンドルの公式 ある既知の関数 f >x を積分区間 a,b@ で積分する場合，分割点 xi >ab@ i1, 2,N の 値を用いて次のように求めることが出来る． ³ N ¦ b # a i dx C i f x i 0 ここで，分割点 ix は一般に積分点と呼ばれる．積分点の数Nがガウス ～ 今月号のイラスト 次元がチガウ数学の天才。 (c) イラストレーション結木さくら 4月の主な誕生人物 01日 親鸞／鎌倉時代の僧 01日 ビスマルク／政治家 01日 浜口雄幸／政治家 02日 アンデルセン／童話作家 02日 ゾラ／小説家 03日 アーヴィング／小説家 03日 長塚節／歌人表31 ガウス・ルジャンドル積分公式 C Fortran90;

磁場公式b 磁場に関するガウスの法則 Lorett

3 13 ガウスの定理

物理公式集 有限区間（a,b）の積分をガウスルジャンドル求積法で計算します。 f(x) 区間 (a, b) 分割数 n;逆に ガウスの定理からグリーンの公式を導くには, ベクトル値関数として をとる このとき だからグリーンの公式が出てくる ガウスは19世紀の数学において他を寄せ付けないく らいの業績をあげた人物であるが, Cross 3 によれば, 彼が見いだしたものは( 4 )の特殊な ものでしかなかったというガウス・ルジャンドル公式による求積 上述のように n 次のこの方法には、 n 次のルジャンドル多項式 P n (x) が対応している。このときの n 次多項式は P n (1) = 1 となるよう正規化され、 i 番目のガウスノード x i は i 番目の P n の根である。

マクスウェル方程式 電磁気学まとめ

ガウス積分について宇宙一わかりやすく解説する 物理学生エンジニア

エクセルを用いたガウス・ルジャンドル積分公式による数値積分 Excelを用いた科学技術計算が第2版になりました 30年10月！ amazon：Excelで操る!図1：ガウス関数（式2）。 σ = 1（細長い方）、σ = 2（幅広い方）。 x軸と囲まれた面積は、σの値によらず1となります。 （式3） ガウス関数の数学的な特徴 （変曲点） x = ±σで変曲点をとります。 （式4） （最大値） x = 0で最大値hをとります。 （式5） ちなみに なので，変曲点における高さは更新日時 ガウス記号 実数 x x x に対し

ガウスの数論世界をゆく 正多角形の作図から相互法則 数論幾何へ 数学書房選書 栗原 将人 桂 利行 栗原 将人 堤 誉志雄 深谷 賢治 本 通販 Amazon

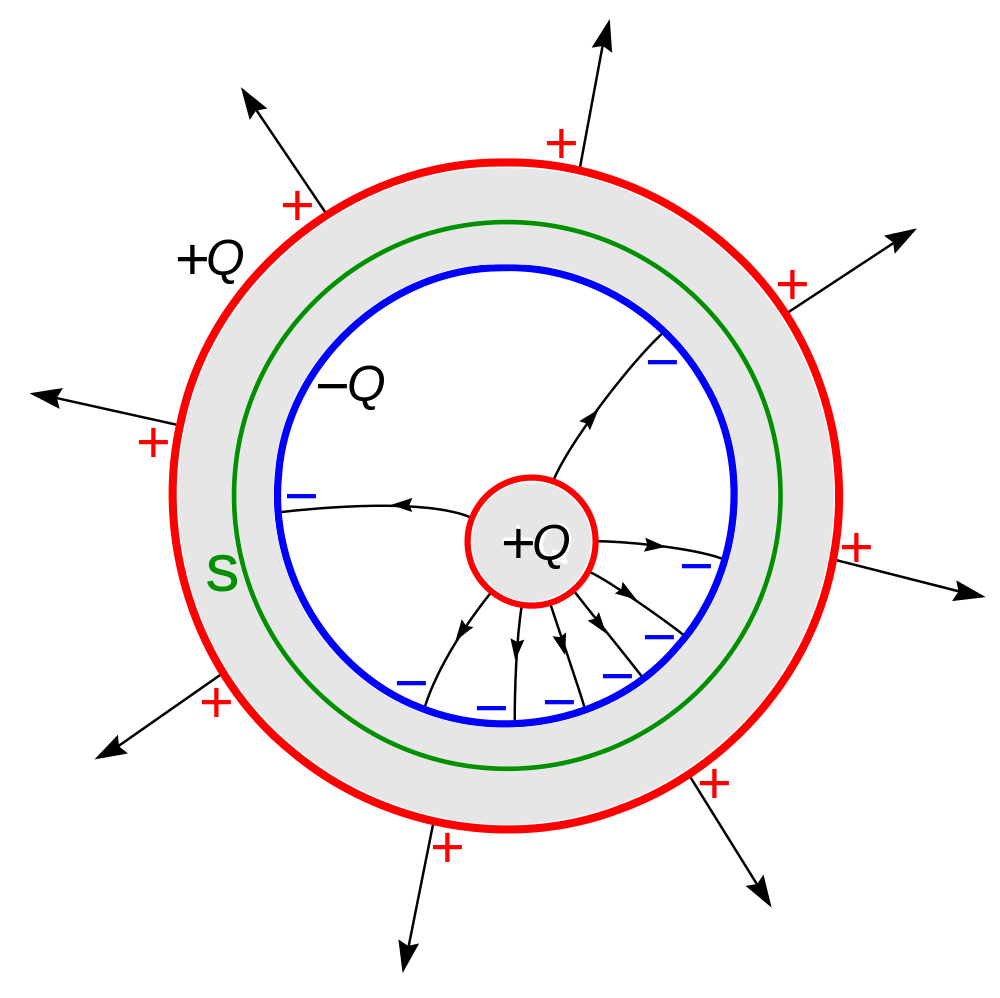
ガウスの法則

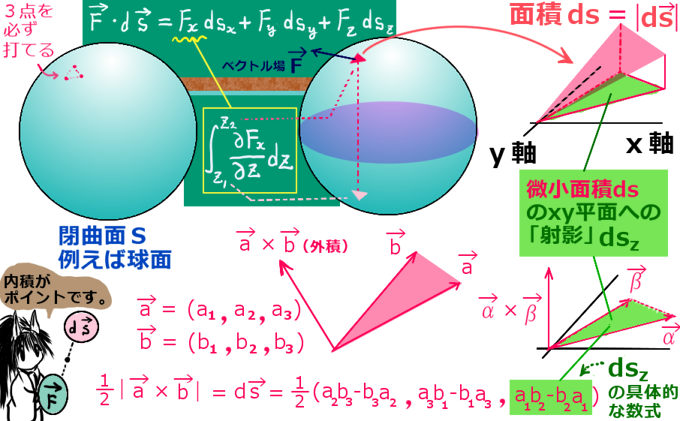
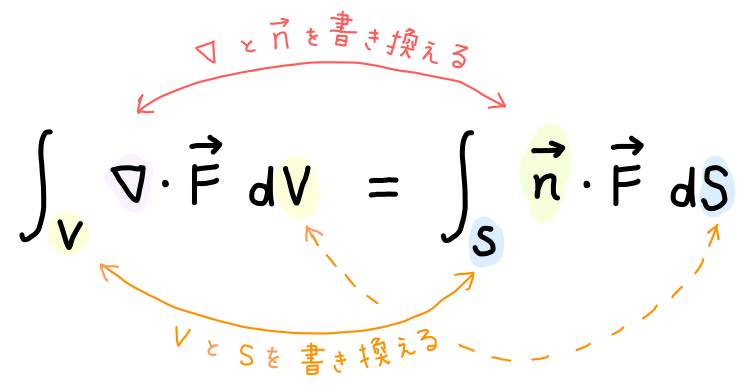
1．ガウス（Gauss）の定理 （1）証明 任意のベクトル関数A（x，y，z）が閉曲面Sの内部で連続であり、divAが内部のどの点でも値を持つ場合には次の関係式が成り立つ。ガウスの定理 ここで、閉曲面の面積要素ベクトルdSは、その大きさが面積値で面に垂直な外向き法線方向を向くとしておりそして、これにガウス積分の公式 \begin{equation} \int_{\infty}^{\infty} e^{ax^{2}} \, dx = \sqrt{\frac{\pi}{a}} \5 ( a \gt 0 ) \label{gauss} \end{equation} を用いれば式\eqref{half}が得られる。式\eqref{half}をガンマ関数の性質\eqref{gamma2}と合わせることによって、半整数の点におけるガンマ関数の値（すなわち半整数の階乗本賞設立の公式発表は02年4月30日、 賞に名前を冠したCarl Friedrich Gaussの生誕225年記念行事で行われた。 この賞は4年に1度の国際数学者会議において授与され、 06年の会議が最初となる。授賞者はIMUの審査委員会によって7月までに選出される。 ガウス(Carl Friedrich Gauss )は全時代を通して

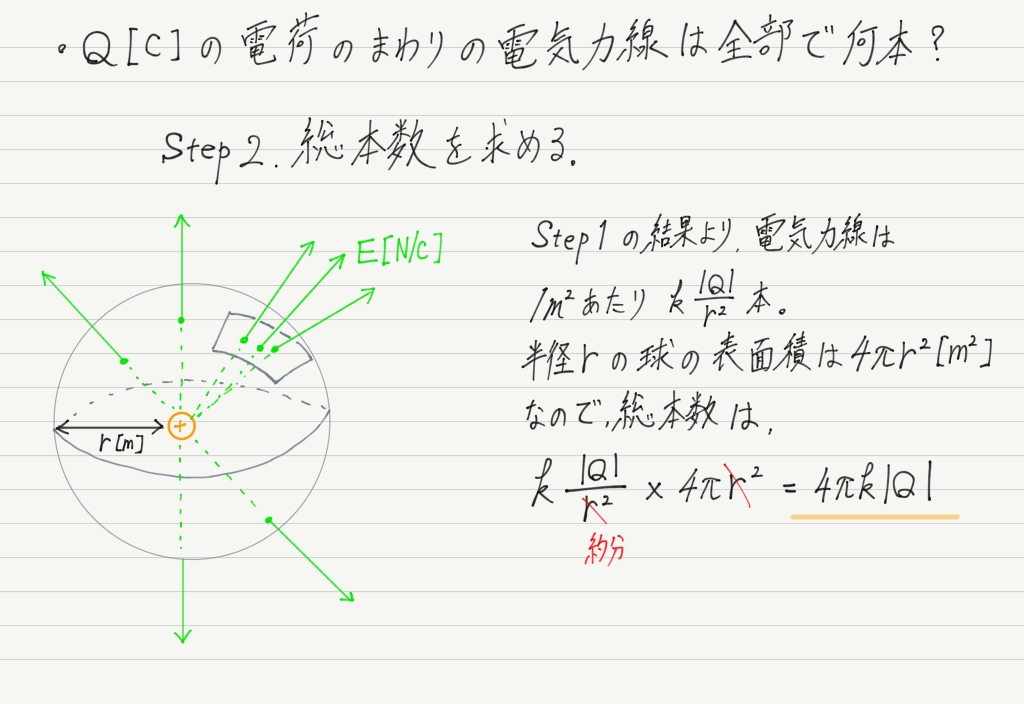
高校物理 電気力線の本数 ガウスの法則 練習編 映像授業のtry It トライイット

ガウスの法則 物理学解体新書

ガウスの積分公式 Gaussian quadrature この組み合わせがよく使用され る。4点におけるfの値を使用し て領域における積分の値を近 似する。 2 ガウスの積分公式 Gaussian quadrature この組み合わせがよく使用され る。4点におけるfの値を使用し て領域における積分の値を近 似する。 10 10 ( ,ここまでできる科学技術計算 神足 史人 定積分は関数、xの区間、x軸で囲まれた領域の面積を63 ガウスの公式(ガウス・ルジャンドル公式) チェビシェフの公式を導き出す時に、係数が同じになるように決めた。 このとき、 x i の値はかなり複雑になって

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

ガウスの法則を解説 Youtube

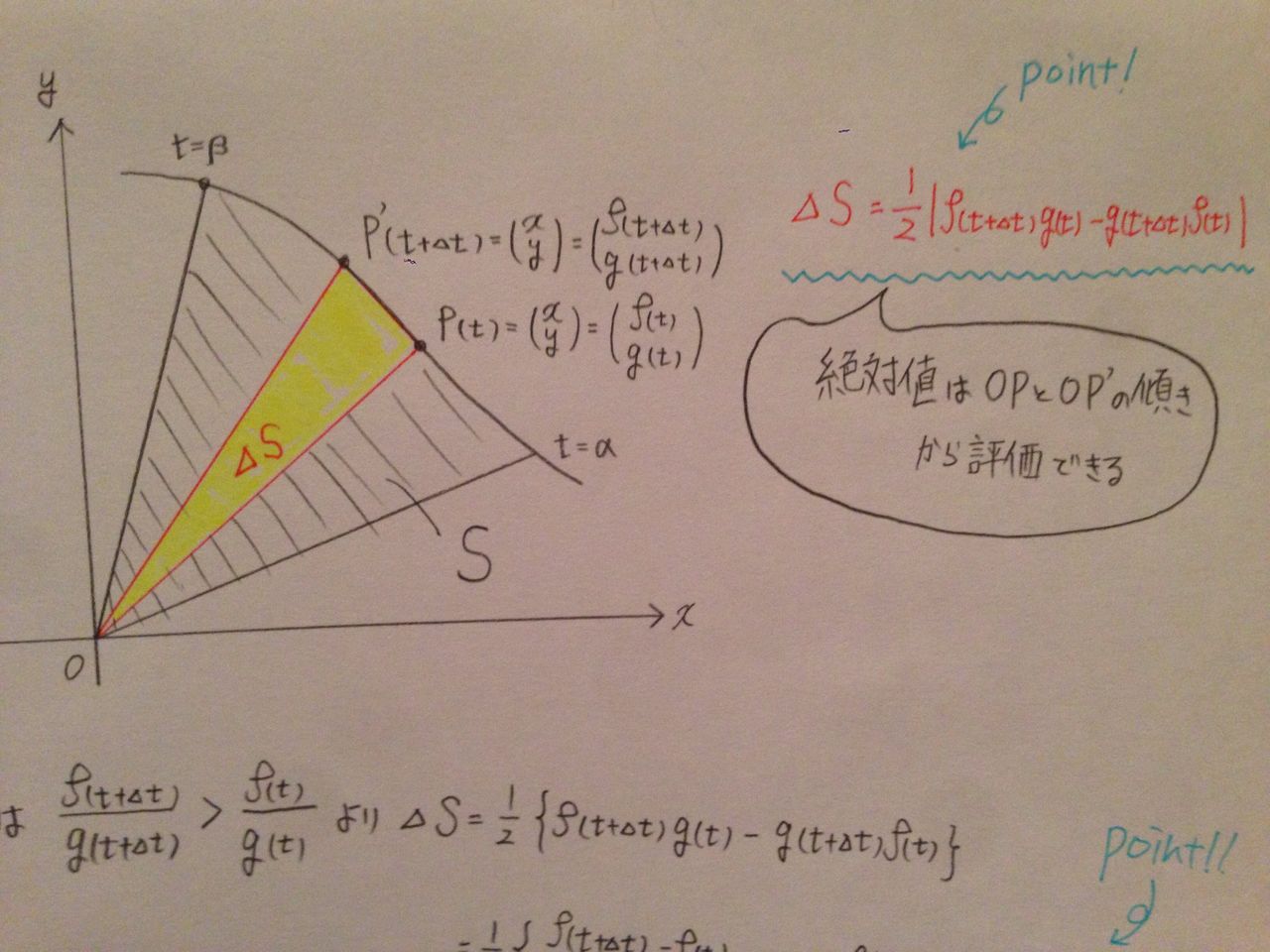
そしてガウスの公式はグリーンの公式とは別のものとして定義される（文献 3 pp など）。 まずは大学流の書き方で述べる。 ガウスの公式 区分的 `C^1` 級正則な曲線 `C` で囲まれた領域 `S` を考える。 ここで、`bbn` を `C` の外向き法線単位ベクトル、`bbF (x, y) = (f(x, y), g(x, y))` を `S`ガウスの法則の公式は数式で書くと複雑に見えるが， 実際での応用例は，ほとんど対称性の良い例に限られている． 例えば は1次元では dE/dx＝r/e 0 であるので答えは E= r/e 0 x定数 である 公式は， その構造を絵画的に理解する方が柔軟な使い方ができる． 6 (1) 微小な直方体 DV=DxDyDz では積分型いて述べた．また，ある具体例に対してガウス及びワインガルテンの公式を偏微分 方程式とみることで行列のスペクトル分解を用いて，曲面の存在に関するボンネの 定理が成り立つことを確認した． 6章では，微分幾何学の金字塔ともいえるガウス・ボンネの定理について，パラ メータ表示が

ガウスの法則 高校物理の備忘録

ガウスの法則 電磁気の基本法則を分かりやすく解説 高校生向け受験応援メディア 受験のミカタ

4 ガウス・グリーンの公式 定理44 Dを有限個のなめらかな曲線で囲まれる有界な閉集合とする． 境界を∂Dと書く．f,gがDでC1級の関数ならば ∂D f(x,y)dxg(x,y)dy= D (∂g ∂x ∂f ∂y) dxdy が成り立つ．ただし，∂Dの向きは進行方向左側にDの内部を見るよう に進むものとする．ガウスの乗法公式 \(n\in\mathbb{N}\)とする。 \ \Gamma(nz)=\frac{n^{nz\frac{1}{2}}}{\left(2\pi\right)^{\frac{n1}{2}}}\prod_{k=0}^{n1}\Gamma\left(z\frac表34 台形公式，シンプソン公式，ガウス・ルジャンドル公式 C Fortran90

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

証明 ガウスの発散定理 理数系無料オンライン学習 Kori

ガウスシアンビーム 光学 Gaussian Beam Optics ガウシアン 分布 は半径方向 に対称 な分布 で、 その 電界変化 は次の式で表わされます。 Rはビーム 中心 からの 距離 として 定義 されま す。 ω0は、 軸上 の頂点 の1/e となるところの 半径 です。表33 ガウス・ルジャンドル積分公式の補間点と重み C Fortran90;06/08/17 · ガウス積分の公式 基本形 eax2の積分 これがガウス積分の基本形ですね。一回計算したことがある方ならわかると思いますが、これはそのままでは計算できません。特別な操作をして2次元で考えた結果からこの公式は導かれています。 まずここまで式変形し

ガウス積分の公式を証明 導出する 微積分 K San Link

ガウスの法則と電気力線 電場が分かる 式の意味を立体的に解説

GaussLegendre求積公式の導出 千葉豪 平成28 年12 月15 日 以下の(N 1)次の多項式f(x)を考える。 f(x) = aN 1x N 1 a N 2x N 2 a 1xa0 (1) この多項式について、区間 1;1の積分を以下のガウス求積（Gaussian quadrature）で求 めるとする。 ∫1 1 f(x)dx = ∑M m=1 f(xm)wm (2) 上式右辺におけるxm が求積公式の離散点、wm がガウスの積分公式 • 無次元化された自然座標系1,1 を対象とする。 •m個の積分点を使用すると（2m1）次の関数まで は近似可能（従って1次，2次の内挿関数（形状関 数）を使用するときは，m=2で十分） m k f d w k f k 1 1 1 =1 =0 =1 , 5/9 3 000, 8/9 2 , 100 1 000, 0 k k k k k k k k w m w m w m wよって 不可能な積分を可能にするテクニック！ガウスさんすごい！ コンテンツへスキップ ナビゲーションに移動 物理公式の証明 ホーム;

ガウスの法則が 閉曲面上を貫く電気力線の本数が比例定数を1 物理に関する質問 勉強質問サイト

講師 幹 浩文 A314 微分 ベクトル解析 14 講師 幹 浩文 A314 A１03 10 50 12 金 Ppt Download

ライノで面の曲率を視覚的にみるときに、曲率分析をします。今回はその内のガウス曲率について少しみていきます。 左がガウス曲率0、真ん中が負のガウス曲率、右が正のガウス曲率をもった曲面。 wikiを参考に説明をしてみると ガウス曲率が正の場合：曲面は楕円点を持っており、曲面は法則の辞典 ガウスの結像公式（球面）の用語解説 曲率半径 r の単一の球面があって，物体までの距離を s，像までの距離を s′，この球面で分割されている二つの媒質の屈折率をそれぞれ n，n′ としたとガウスの計算法とは ガウスの計算法とは、ドイツの天才数学者ガウスが「1 から 100 までの数字すべてを足すように」と課題を出された際に、単純に1から100までを足していくのではなく、1と100の和である101が50個あるからだと瞬時に答えを出したというものです。

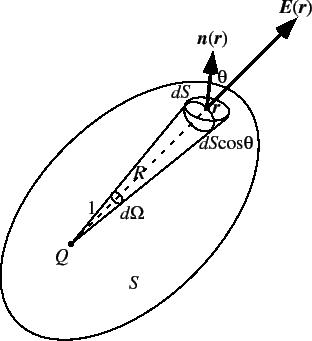
積分形のガウスの法則

ガウスの法則語呂合わせ コンデンサーと電場は 剣道の試合で 18岩手大第3問より 電磁気 入試物理を語呂合わせで解く大学入試ゴロ物理

∞ −∞ dxe−αx2 = π α の導出。 左辺をI と置いて、I2 を計算すると I ≡!06/03/21 · ガウス積分は，統計学や物理学で登場する有名な定積分の公式です。この記事では， ガウス積分の2通りの証明方法 と， ガウス積分の応用 について詳しく解説します。∞ −∞ dye−α(x2y2) I2 の計算で、同じ積分変数を使ってはいけないことに注意。 2次元極座標(x,y)=(rcosθ,rsinθ)

ガウス関数の手抜き理解 大人になってからの再学習

発散を使ったガウスの発散定理について教えてください この辺見ればわかる Yahoo 知恵袋

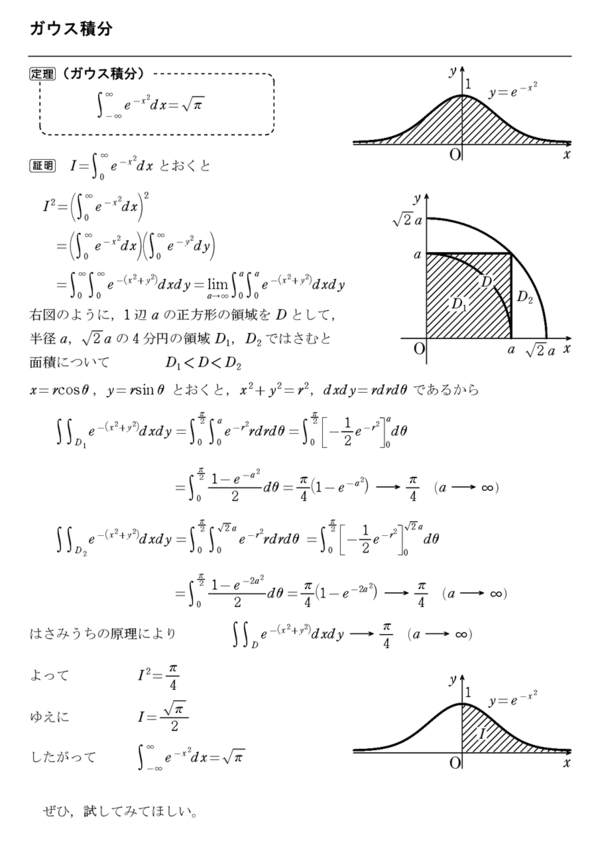
ガウス積分の公式の証明 いくら公式だとはいっても，一度は本当にそうなることを確認しておきたいものです． この公式の証明は院試で頻出ですので，その道を目指す方は覚えておくと良いでしょう． まず，左辺の積分値を とします．

ガウス積分の公式集 証明付 理数アラカルト

ガウスの法則

高校数学a ガウス記号 X の方程式 受験の月

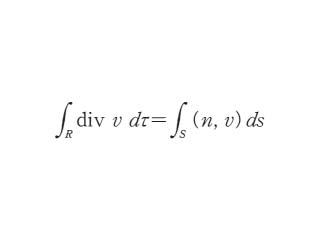
ガウスの定理とは コトバンク

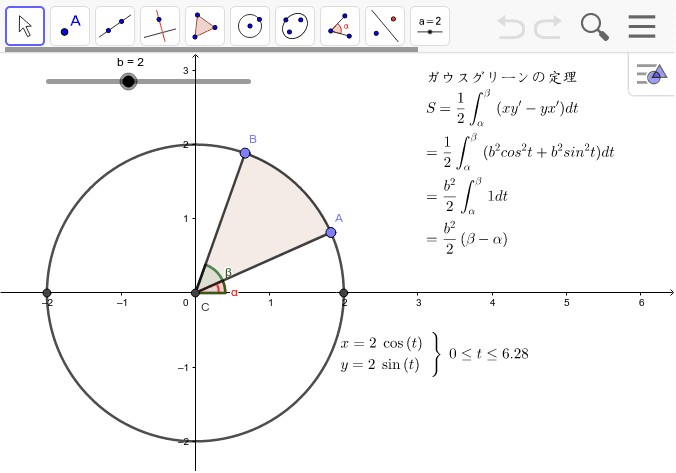
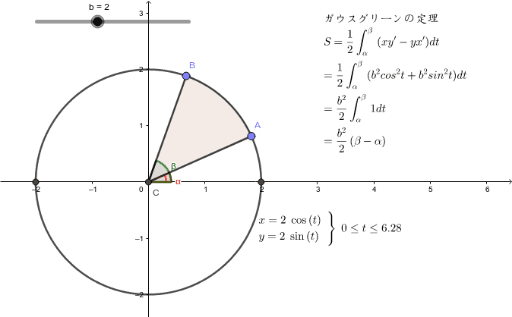
ガウスグリーンの定理 Geogebra

高校物理 ガウスの法則 Youtube

N 大学工学部電気電子工学科 郡山 電磁気学

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

ガウス記号を含む式の値を求める入試問題 18年 富山大 大学入試数学の考え方と解法

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

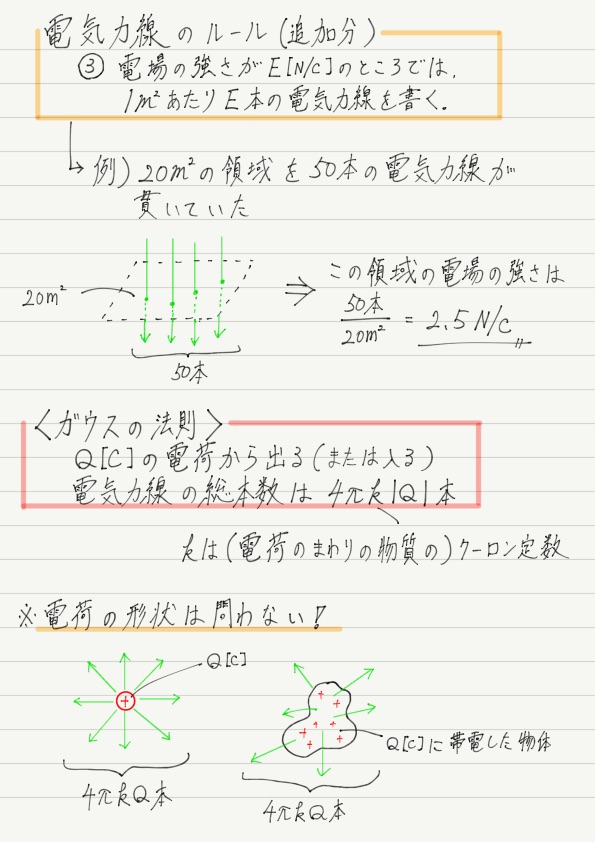
ガウスの法則 高校物理をあきらめる前に 高校物理をあきらめる前に

ガウス積分の公式集 証明付 理数アラカルト

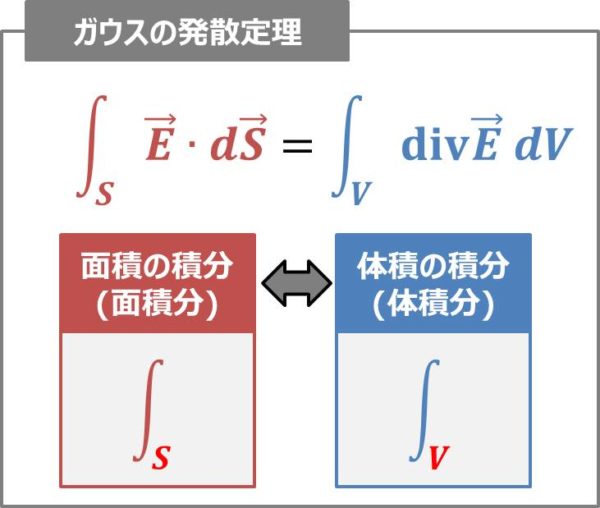
ガウスの発散定理とは 公式 や 意味 などを解説

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門

ガウス積分の公式集 証明付 理数アラカルト

ガウスの法則 電磁気の基本法則を分かりやすく解説 高校生向け受験応援メディア 受験のミカタ

テラスハウス ガウス グリーンの定理 理系 落ちこぼれkの東大受験日記

グリーンの定理 積分定理の王

ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門

マクスウェル方程式 電磁気学まとめ

ガウスの法則 高校物理の備忘録

ガウス積分はどうやって求める 極座標変換による計算

ガウス積分の公式 物理のかぎしっぽ

ガウス積分の公式の２通りの証明 高校数学の美しい物語

高校物理 ガウスの法則を制する者は受験を制す 偏差値40プログラマー

Gaussの定理

ガウスの法則とアンペールの法則 Mitty Ph D Note

ガウス積分の公式集 証明付 理数アラカルト

ガウスの法則語呂合わせ コンデンサーと電場は 剣道の試合で 18岩手大第3問より 電磁気 入試物理を語呂合わせで解く大学入試ゴロ物理

ガウスグリーンの定理 Geogebra

ガウス関数の積分公式について

ガウス ルジャンドルの公式によるpの計算 Commutative Weblog 5

高校物理公式集 電場 ガウスの法則 Tekibo

第５話 あっと驚くガウスの数値積分法 Femingway

ガウスグリーンの定理の応用 Geogebra

ガウスの法則 高校物理の備忘録

グリーンの定理 積分定理の王

ガウスの法則

フーリエ変換の公式と導出 Notes Jp

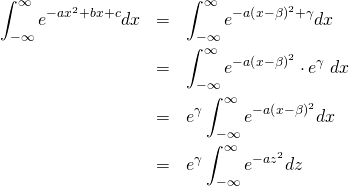
ガウス積分の公式を証明 導出する 微積分 K San Link

ガウスの発散定理 ベクトル解析 基礎からの数学入門

ガウス積分 Wikipedia

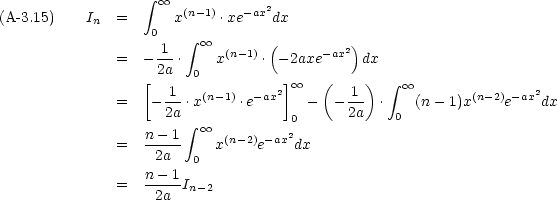
ａ ３ Gauss 関数の積分

ガウスの発散定理 微小要素のイメージから分かりやすく証明 スモビュ

ガウス積分と派生公式 Notes Jp

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門

ガウス積分による近似を使った スターリングの公式について なぜn 1の 数学 教えて Goo

電界と電位 ガウスの法則 電験3種 理論 最速合格

ガウス積分をウォリスの公式等から導く Youtube

Undergraduate数学的統計学 物理学 ガウス積分公式 筆記 Clear

グリーンの定理 積分定理の王

ガウス積分の公式集 証明付 理数アラカルト

１４章 ベクトルの発散とガウスの発散定理とグリーンの定理

ガウス関数のモーメントを簡単に計算する方法 物理のかぎしっぽ

ガウスの法則 高校物理をあきらめる前に 高校物理をあきらめる前に

複素関数版ガウス積分 フレネル積分 Youtube

ガウス積分の公式 物理のかぎしっぽ

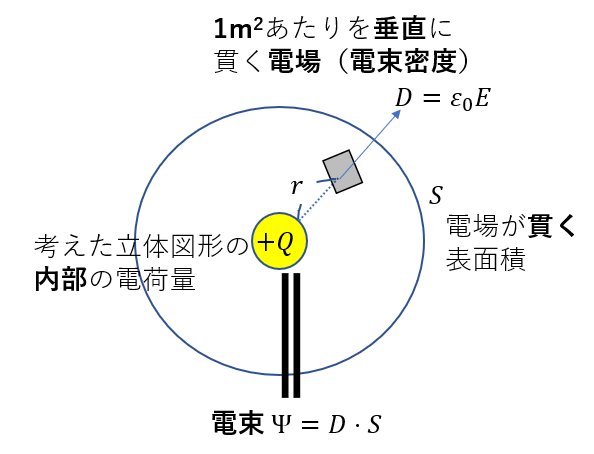
ガウスの公式の積分形について 左の式は出ていく量右側は内 Yahoo 知恵袋

ガウスの法則とは 公式 や 積分形 や 微分形 などを解説

ベクトル解析 わかりやすい 発散 Div のイメージ ガウスの発散定理 の証明 ばたぱら

ガウスの発散定理の応用について のような公式は物理学においてどのよ Yahoo 知恵袋

Prml 2 3 1 2 3 3

ガウシアンビームの伝播 2 Optronics Online オプトロニクスオンライン

電磁気学 電気力線とガウスの法則 例題付き Cupuasu クプアス

ガウス ボネの定理 Wikipedia

偏微分公式証明 3 Cpdpg

グリーンの定理 積分定理の王

電磁気の公式を総まとめしてみた 受験物理 Set Up

復活祭の日取りの算出法 ガウスの公式そのほか 新井正夫 著 古書 往来座 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

平方剰余の相互法則の証明 ガウス和を用いた方法 Tsujimotterのノートブック

ガウスの法則と公式 例題 理系ラボ

ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門

ガウス積分 怜悧玲瓏 高校数学を天空から俯瞰する

ガウスの法則と公式 例題 理系ラボ